A/B Testing - A POC for User Research

This case study reviews a proof of concept for an app to run an A/B test with large sets of data comparing promotion performance of a new service.

The Problem

This new service is groundbreaking and the company wanted to promote it so that they could maximize sales, but was having a hard time deciding between which promotion to go with.

The Solution

In order to determine which promotion has the greatest effect on sales, an A/B test was designed to learn which of the promotions had the greatest effect on sales. Several potential customers were were randomly selected from a larger target audience and the new service was introduced using one of three promotions for four weeks. With this data, promotion performance can be analyzed to provide a data-driven direction to maximize the ROI. This was done through a proof of concept application which was created using Python, some math and a statistics model.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import ttest_ind, chisquare

Defining Hypotheses

The question is "which of the promotions performs the best at driving sales?". In order to answer this question, it can be posed as a differentiating hypothesis (in this case 3 separate hypotheses).

Promotion A vs. B

Null hypothesis: There is not a significant difference in total sales between promotions A and B.
Alternative hypothesis: There is a significant difference in total sales between promotions A and B.

Promotion B vs. C

Null hypothesis: There is not a significant difference in total sales between promotions B and C.
Alternative hypothesis: There is a significant difference in total sales between promotions B and C.

Promotion A vs. C

Null hypothesis: There is not a significant difference in total sales between promotions A and C.
Alternative hypothesis: There is a significant difference in total sales between promotions A and C.

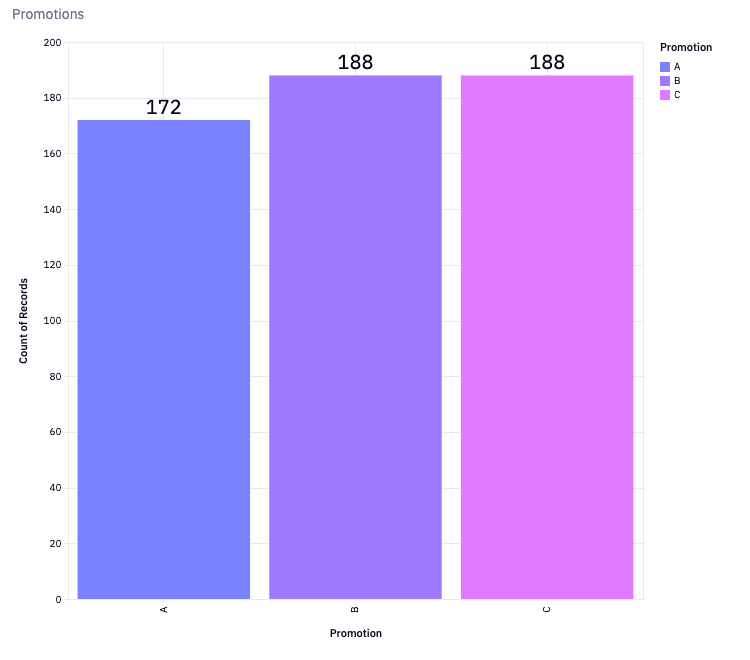
Balancing Data

Each promotion was well planned out and each of the targeted customers saw around 1/3 of the total traffic. However, things happen and confirmation that the results reflect this balance is needed. Stability of the groups can be verified by plotting their distributions in a chart.

1
2
3

ratioA = data[data["Promotion"] == "A"]["SalesInThousands"].count() / data.shape[0]
ratioB = data[data["Promotion"] == "B"]["SalesInThousands"].count() / data.shape[0]
ratioC = data[data["Promotion"] == "C"]["SalesInThousands"].count() / data.shape[0]

31.39%

Viewed Promotion A

34.31%

Viewed Promotion B

34.31%

Viewed Promotion C

SRM Check

Looks like each promotion was presented to roughly 34% of customers with promotion A being slightly under that. It would be a shame if this minor disproportion threw off the entire hypothesis test so a quick check is needed to see if this imbalance is significant or not. A technique called sample ratio mismatch or SRM for short to verify any imbalance.

def SRM(dataframe):
  promo1 = dataframe["Promotion"].value_counts().loc["A"]
  promo2 = dataframe["Promotion"].value_counts().loc["B"]
  promo3 = dataframe["Promotion"].value_counts().loc["C"]

  # creates a list of the obsereved values
  observed = [ promo1, promo2, promo3 ]

  # calculates the sum of all observations
  total = sum(observed)

  # the expected value is the total divided by 3 (for each promo)
  expected = [ total/3, total/3, total/3 ]

  # do the chi square test and return the results
  chi = chisquare(observed, f_exp=expected)[1]
  if chi &lt; 0.01:
    result = 'SRM detected'
  else:
    result = 'No SRM detected'

  return promo1, promo2, promo3, chi, result

  p1, p2, p3, score, result = SRM(data)

0.626784

No SRM detected (p-value)

Comparing Promotions

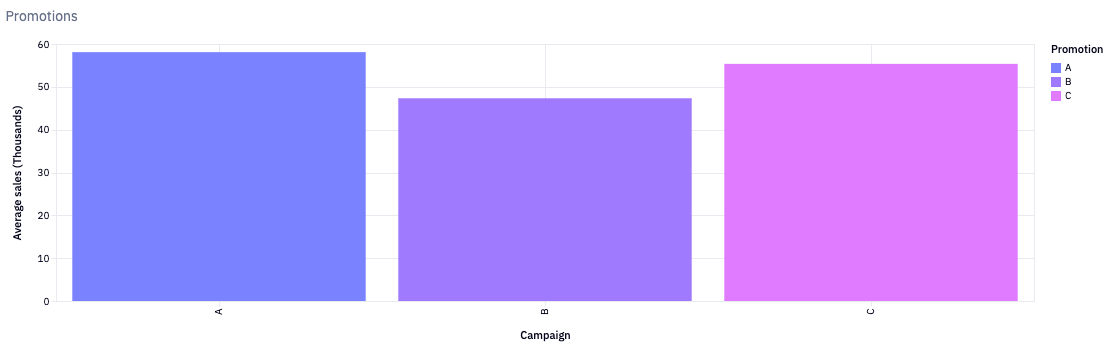
An idea of how each campaign has performed thus far can be gathered by comparing the average sales per promotion. The chart below shows us two visual representations of how each group compares to each other and it looks like campaign A takes 1st place 🥇. Further analysis was needed to confirm the difference between the 3 campaigns.

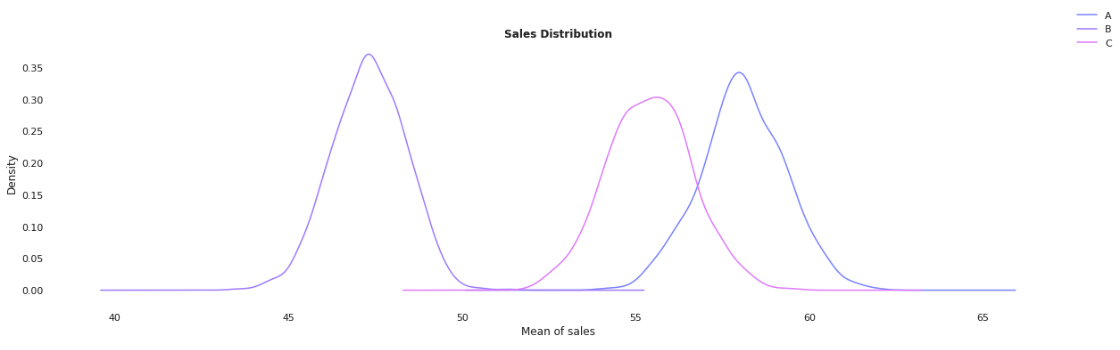
KDE Plot

Utilizing a kernel density estimate, it is much more apparent that there is a difference between each of our groups. Notice how campaign A and C are fairly close to each other while promotion B is left behind.

Conducting Tests

Answering the question "Are the differences I'm seeing really there or is it just due to randomness" requires a statistical test. Using an independent t-test, a determination of whether or not the differences between promotions are indeed significant or just random fluctuations.

def test(A, B):
  p = ttest_ind(A, B)[1]
  significance_level = 0.05

  if p > significance_level:
    result = f'no significant difference. [p-value = {round(p, 4)}]'
  else:
    result = f'significant difference. [p-value = {round(p, 4)}]'
  return result

groupA = data[data['Promotion'] == 'A']['SalesInThousands']
groupB = data[data['Promotion'] == 'B']['SalesInThousands']
groupC = data[data['Promotion'] == 'C']['SalesInThousands']

print(f"A/B campaign has {test(groupA, groupB)}")
print(f"B/C campaign has {test(groupB, groupC)}")
print(f"A/C campaign has {test(groupA, groupC)}")

Results

The results showed that the p-value of the A/B and B/C tests were 0 and the p-value for the A/C test was 0.120, meaning that there is no difference in sales between the A and C promotions. This means that the difference we see between the A and C promotion is not significant and either promotion would perform well in sales. This also means that it's safe to conclude that promotion A out performed promotion B and that promotion C out performed promotion B.

Deriving Meaning from Results

Comparing A/B Promotions

There was a significant difference between the A and B promotions.

Comparing B/C Promotions

There was a significant difference between the B and C promotions.

Comparing A/C Promotions

There was not a significant difference between the A and C promotions.

Recommendation

Due to the results of the A/B/C test and by the process of elimination, promotion B had the least impact on sales when compared to promotions A and C, and promotion B could be removed from consideration. This left promotions A and C, which had no significant difference when considering sales, although promotion A was more profitable. With this in mind, a recommendatoin to go with campaign A was made. However, either promotion would work just as well and perhaps a variety of equally performing promotions would be beneficial.